원의 면적을 계산하는 방법. 원의 면적 : 공식
서클에는 보다 신중한 접근이 필요하며 작업 B5에서는 훨씬 덜 일반적입니다. 동시에, 일반적인 해법 체계는 다각형의 경우보다 훨씬 간단합니다("좌표 격자의 다각형 영역" 단원 참조).
이러한 작업에 필요한 것은 원 R의 반지름을 찾는 것뿐입니다. 그런 다음 S = πR 2 공식을 사용하여 원의 면적을 계산할 수 있습니다. 또한 이 공식에서 이를 해결하려면 R 2를 찾는 것으로 충분합니다.
표시된 값을 찾으려면 그리드 선의 교차점에 있는 원의 점을 표시하는 것으로 충분합니다. 그리고 피타고라스 정리를 이용해보세요. 반경 계산의 구체적인 예를 살펴보겠습니다.
일. 그림에 표시된 세 원의 반지름을 찾으세요.
각 원에서 추가 구성을 수행해 보겠습니다.
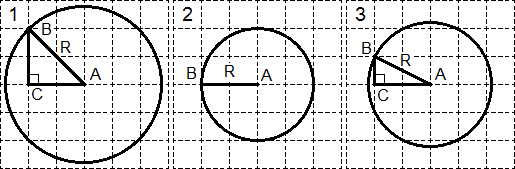
각각의 경우에 점 B는 원에서 그리드 선의 교차점에 놓이도록 선택됩니다. 원 1과 3의 점 C는 그림을 직각삼각형으로 완성합니다. 반경을 찾는 것이 남아 있습니다.
첫 번째 원에서 삼각형 ABC를 생각해 보세요. 피타고라스 정리에 따르면: R 2 = AB 2 = AC 2 + BC 2 = 2 2 + 2 2 = 8.
두 번째 원의 경우 모든 것이 명확합니다: R = AB = 2.
세 번째 경우도 첫 번째 경우와 비슷합니다. 피타고라스 정리를 사용한 삼각형 ABC에서: R 2 = AB 2 = AC 2 + BC 2 = 1 2 + 2 2 = 5.
이제 우리는 원(또는 적어도 사각형)의 반지름을 찾는 방법을 알았습니다. 그러므로 우리는 그 지역을 찾을 수 있습니다. 전체 원이 아닌 섹터의 영역을 찾아야 하는 문제가 있습니다. 그러한 경우 이 섹터가 원의 어느 부분인지 쉽게 알 수 있으므로 영역을 찾을 수 있습니다.
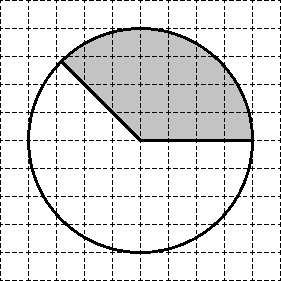
일. 음영처리된 부분의 면적 S를 찾으세요. 답에 S/π를 표시해 주십시오.
분명히 섹터는 원의 1/4입니다. 따라서 S = 0.25 S 원입니다.
원의 면적인 원의 S를 찾는 것이 남아 있습니다. 이를 위해 추가 구성을 수행합니다.
삼각형 ABC는 직각삼각형입니다. 피타고라스 정리에 따르면 R 2 = AB 2 = AC 2 + BC 2 = 2 2 + 2 2 = 8입니다.
이제 원과 섹터의 면적을 찾습니다. S 원 = πR 2 = 8π ; S = 0.25 S 원 = 2π.
마지막으로 원하는 값은 S /π = 2입니다.
반경을 알 수 없는 섹터 영역
이것은 완전히 새로운 유형의 작업이며 2010-2011년에는 이와 같은 것이 없었습니다. 조건에 따라 특정 면적(즉, 반경이 아닌 면적!)의 원이 주어집니다. 그런 다음 이 원 안에는 영역을 찾아야 하는 섹터가 선택됩니다.
좋은 소식은 이러한 문제가 수학 통합 국가 시험에 나타나는 모든 영역 문제 중에서 가장 쉽다는 것입니다. 또한 원과 부채꼴은 항상 좌표 격자 위에 배치됩니다. 따라서 이러한 문제를 해결하는 방법을 알아보려면 그림을 살펴보십시오.

원래 원의 면적이 S = 80이라고 가정합니다. 그런 다음 각각 면적 S = 40인 두 개의 섹터로 나눌 수 있습니다(2단계 참조). 마찬가지로 각 "반쪽" 섹터는 다시 절반으로 나눌 수 있습니다. 즉, 각각 면적 S = 20인 4개의 섹터를 얻습니다(3단계 참조). 마지막으로, 각 섹터를 두 개로 더 나눌 수 있습니다. 즉, 8개의 "스크랩" 섹터를 얻게 됩니다. 이러한 "스크랩" 각각의 면적은 S = 10입니다.
참고: USE 수학 문제에는 더 미세한 구분이 없습니다! 따라서 문제 B-3을 해결하기 위한 알고리즘은 다음과 같습니다.
- 원래 원을 8개의 "스크랩" 섹터로 자릅니다. 각각의 면적은 전체 원 면적의 정확히 1/8입니다. 예를 들어 조건에 따라 원의 면적 S가 240이면 "스크랩"의 면적은 S = 240입니다. 8 = 30;
- 원래 섹터에 얼마나 많은 "스크랩"이 들어 있는지 알아보십시오. 해당 영역을 찾아야합니다. 예를 들어, 우리 섹터에 면적이 30인 3개의 "스크랩"이 포함되어 있는 경우 원하는 섹터의 면적은 S = 3 · 30 = 90입니다. 이것이 답이 될 것입니다.
그게 다야! 문제는 실질적으로 구두로 해결됩니다. 그래도 뭔가 명확하지 않다면 피자를 사서 8조각으로 자르세요. 이러한 각 조각은 더 큰 조각으로 결합될 수 있는 동일한 섹터, 즉 "스크랩"이 됩니다.
이제 통합 상태 시험 평가판의 예를 살펴보겠습니다.
일. 체크무늬 종이에 면적 40의 원을 그립니다. 음영처리된 그림의 면적을 구합니다.
따라서 원의 면적은 40입니다. 이를 8개의 섹터로 나눕니다. 각 섹터의 면적은 S = 40: 5 = 8입니다. 우리는 다음을 얻습니다.
분명히 음영처리된 섹터는 정확히 두 개의 "스크랩" 섹터로 구성됩니다. 따라서 면적은 2 · 5 = 10입니다. 이것이 전체 해결책입니다!
일. 체크무늬 종이에 면적이 64인 원을 그립니다. 음영처리된 그림의 면적을 구합니다.
다시, 전체 원을 8개의 동일한 섹터로 나눕니다. 분명히 그 중 하나의 영역이 정확히 찾아야 할 영역입니다. 따라서 면적은 S = 64: 8 = 8입니다.
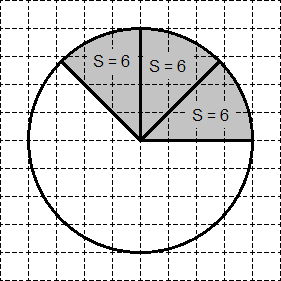
일. 체크무늬 종이에 면적이 48인 원을 그립니다. 음영처리된 그림의 면적을 구합니다.
다시 원을 8개의 동일한 섹터로 나눕니다. 각각의 면적은 S = 48: 8 = 6과 같습니다. 필요한 섹터에는 정확히 3개의 "스크랩" 섹터가 포함됩니다(그림 참조). 따라서 필요한 섹터의 면적은 3 6 = 18입니다.
학교 커리큘럼에서 알 수 있듯이 원은 일반적으로 그림의 중심에서 등거리에 있는 많은 점으로 구성된 평면 기하학적 도형이라고 합니다. 모두 같은 거리에 있기 때문에 원을 형성합니다.
기사를 통한 편리한 탐색: