직사각형의 이등분선은 무엇입니까? 삼각형 ABC의 기본 요소

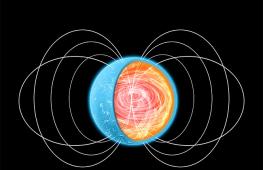
삼각형의 이등분선은 삼각형의 각을 두 개의 동일한 각으로 나누는 선분입니다. 예를 들어, 삼각형의 각도가 120°라면 이등분선을 그려 각각 60°인 두 개의 각도를 구성합니다.

그리고 삼각형에는 세 각이 있으므로 세 개의 이등분선을 그릴 수 있습니다. 모두 하나의 컷오프 지점이 있습니다. 이 점은 삼각형에 새겨진 원의 중심입니다. 다른 방법으로 이 교차점을 삼각형의 내심이라고 합니다.

내부 각도와 외부 각도의 두 이등분선이 교차하면 90 0 각도가 얻어집니다. 삼각형의 외각은 삼각형의 내각에 인접한 각도입니다.

쌀. 1. 3개의 이등분선을 포함하는 삼각형

이등분선은 반대쪽을 양쪽에 연결된 두 개의 세그먼트로 나눕니다.

$$(CL\오버(LB)) = (AC\오버(AB))$$

이등분선은 각의 변에서 등거리에 있습니다. 즉, 이등분선은 각의 변에서 같은 거리에 있습니다. 즉, 이등분선의 임의의 점에서 삼각형 각도의 각 변에 수직을 떨어뜨리면 이러한 수직은 동일합니다..

한 꼭지점에서 중앙값, 이등분선, 높이를 그리면 중앙값이 가장 긴 세그먼트가 되고 높이는 가장 짧아집니다.

이등분선의 일부 속성

특정 유형의 삼각형에서 이등분선은 특별한 속성을 갖습니다. 이것은 주로 이등변삼각형에 적용됩니다. 이 그림에는 두 개의 동일한 변이 있고 세 번째 변을 밑면이라고 합니다.

이등변삼각형의 꼭지점에서 밑변까지 이등분선을 그리면 높이와 중앙값의 속성을 모두 갖게 됩니다. 따라서 이등분선의 길이는 중앙값의 길이와 높이와 일치합니다.

정의:

  • 키- 삼각형의 꼭지점에서 반대편으로 그어진 수직선입니다.
  • 중앙값– 삼각형의 꼭지점과 대변의 중앙을 연결하는 선분.

쌀. 2. 이등변삼각형의 이등분선

이는 정삼각형, 즉 세 변이 모두 같은 삼각형에도 적용됩니다.

예시 할당

삼각형 ABC에서 BR은 이등분선이고 AB = 6cm, BC = 4cm, RC = 2cm입니다. 세 번째 변의 길이를 뺍니다.

쌀. 3. 삼각형의 이등분선

해결책:

이등분선은 삼각형의 변을 특정 비율로 나눕니다. 이 비율을 이용해서 AR을 표현해 봅시다. 그런 다음 세 번째 변의 길이를 이등분선으로 나눈 선분의 합으로 구합니다.

  • $(AB\오버(BC)) = (AR\오버(RC))$
  • $RC=(6\over(4))*2=3cm$

그러면 전체 세그먼트 AC = RC+ AR

AC = 3+2=5cm.

받은 총 평점: 107.

삼각형 각도의 이등분선은 무엇입니까? 이 질문에 대해, 잘 알려진 쥐가 모퉁이를 돌며 모퉁이를 반으로 나누는 것이 어떤 사람들의 입에서 나온다고 합니다." 만약 대답이 "유머러스하다"라면 아마도 그것이 맞을 것입니다. 그러나 과학적인 관점에서 보면 관점에서 보면, 이 질문에 대한 대답은 다음과 같아야 합니다: 각도의 꼭대기에서 시작하여 후자를 두 개의 동일한 부분으로 나누는 것입니다." 기하학에서 이 그림은 삼각형의 반대편과 교차할 때까지 이등분선의 한 부분으로 인식됩니다. 이것은 오해가 아닙니다. 각도의 이등분선에 대해 정의 외에 또 무엇이 알려져 있나요?

기하학적인 점의 궤적과 마찬가지로 고유한 특성이 있습니다. 그 중 첫 번째는 오히려 부호가 아니라 다음과 같이 간략하게 표현할 수있는 정리입니다. “반대편을 이등분선으로 두 부분으로 나누면 그 비율은 큰 삼각형의 변들.”

두 번째 속성은 모든 각도의 이등분선의 교차점을 내심이라고 합니다.

세 번째 기호: 삼각형의 한 내각과 두 외각의 이등분선은 세 개의 내접원 중 하나의 중심에서 교차합니다.

삼각형 각도의 이등분선의 네 번째 속성은 각 각도가 같으면 후자가 이등변이라는 것입니다.

다섯 번째 기호는 또한 이등변 삼각형과 관련이 있으며 이등분선으로 그림을 인식하기 위한 주요 지침입니다. 즉, 이등변 삼각형에서는 중앙값과 고도 역할을 동시에 수행합니다.

각도의 이등분선은 나침반과 눈금자를 사용하여 구성할 수 있습니다.

여섯 번째 규칙은 정육면체의 2배, 원의 제곱, 각의 삼등분을 이 방식으로 구성하는 것이 불가능한 것과 마찬가지로 기존의 이등분선만으로 후자를 사용하여 삼각형을 구성하는 것이 불가능하다는 것입니다. 엄밀히 말하면 이것들은 모두 삼각형의 각의 이등분선의 속성입니다.

이전 단락을주의 깊게 읽었다면 아마도 한 문구에 관심이 있었을 것입니다. "각도의 삼등분이란 무엇입니까?" -아마 물어볼 것입니다. 삼등분선은 이등분선과 조금 비슷하지만 후자를 그리면 각도가 2등분으로 나누어지고, 삼등분선을 구성할 때에는 3등분하게 됩니다. 당연히 각의 이등분선은 학교에서 가르치지 않기 때문에 기억하기가 더 쉽습니다. 그러나 완전성을 위해 그것에 대해서도 말씀 드리겠습니다.

이미 말했듯이 삼등분선은 컴퍼스와 자로만 구성할 수 없지만 후지타의 법칙과 일부 곡선(파스칼의 달팽이, 사각형, 니코메데스의 원추형, 원뿔 단면, 등)을 사용하여 만들 수 있습니다.

각도의 삼등분에 관한 문제는 네브시스를 사용하여 매우 간단하게 해결됩니다.

기하학에는 각도 삼등분선에 관한 정리가 있습니다. 몰리의 정리라고 합니다. 그녀는 중앙에 있는 각 삼등분선의 교차점이 정점이 될 것이라고 말합니다.

큰 삼각형 안의 작은 검은색 삼각형은 항상 정삼각형입니다. 이 정리는 1904년 영국의 과학자 프랭크 몰리(Frank Morley)에 의해 발견되었습니다.

각도 나누기에 대해 배울 수 있는 내용은 다음과 같습니다. 각도의 삼등분선과 이등분선에는 항상 자세한 설명이 필요합니다. 그러나 여기에는 내가 아직 공개하지 않은 많은 정의가 주어졌습니다. 파스칼의 달팽이, 니코메데스의 콘코이드 등이 있습니다. 이에 대해 쓸 내용이 훨씬 더 많으니 안심하세요.

중등학교의 수많은 과목 중에 '기하학'과 같은 과목이 있습니다. 전통적으로 이 체계적인 과학의 창시자는 그리스인이라고 믿어졌습니다. 오늘날 그리스 기하학은 평면, 직선, 삼각형과 같은 가장 단순한 형태에 대한 연구를 시작한 사람이기 때문에 초등 기하학이라고 불립니다. 우리는 후자나 오히려 이 그림의 이등분선에 관심을 집중할 것입니다. 이미 잊어버린 사람들을 위해 삼각형의 이등분선은 삼각형 모서리 중 하나의 이등분선으로, 이를 반으로 나누고 꼭지점을 반대편에 있는 점과 연결합니다.

삼각형의 이등분선에는 특정 문제를 해결할 때 알아야 할 여러 가지 속성이 있습니다.

  • 각의 이등분선은 각에 인접한 변으로부터 동일한 거리에 위치한 점의 자취입니다.
  • 삼각형의 이등분선은 각도의 반대쪽 변을 인접한 변에 비례하는 세그먼트로 나눕니다. 예를 들어, 이등분선이 각도 K에서 나오는 삼각형 MKB가 주어지면 이 각도의 꼭지점을 반대편 MB의 점 A와 연결합니다. 이 속성과 삼각형을 분석한 결과 MA/AB=MK/KB가 나왔습니다.
  • 삼각형의 세 각의 이등분선이 모두 교차하는 점은 같은 삼각형에 내접하는 원의 중심입니다.
  • 하나의 외각과 두 개의 내각의 이등분선의 밑변은 동일한 직선 위에 있습니다. 단, 외각의 이등분선은 삼각형의 반대쪽 변과 평행하지 않습니다.
  • 만약 하나의 두 이등분선이 있다면 이것은

세 개의 이등분선이 주어지면 나침반을 사용해도 삼각형을 만드는 것이 불가능하다는 점에 유의해야 합니다.

문제를 풀 때 삼각형의 이등분선을 알 수 없지만 길이를 결정해야 하는 경우가 많습니다. 이 문제를 해결하려면 이등분선으로 이등분되는 각도와 이 각도에 인접한 변을 알아야 합니다. 이 경우 필요한 길이는 모서리에 인접한 변의 두 배와 모서리에 인접한 변의 합을 반으로 나눈 각도의 코사인 곱의 비율로 정의됩니다. 예를 들어, 동일한 삼각형 MKB가 주어집니다. 이등분선은 각도 K에서 나오고 점 A에서 MV의 반대쪽과 교차합니다. 이등분선이 나타나는 각도는 y로 표시됩니다. 이제 단어로 말하는 모든 것을 공식의 형태로 적어 보겠습니다: KA = (2*MK*KB*cos y/2) / (MK+KB).

삼각형의 이등분선이 나타나는 각도의 값을 알 수 없지만 모든 변을 알고 있는 경우 이등분선의 길이를 계산하기 위해 추가 변수를 사용합니다. 이 변수를 반주위라고 부르며 다음과 같이 표시합니다. 문자 P: P=1/2*(MK+KB+MB). 그런 다음 이등분선의 길이를 결정하는 이전 공식을 일부 변경합니다. 즉, 분수의 분자에서 모서리에 인접한 변의 길이와 반 둘레의 곱을 두 배로 넣습니다. 반 둘레에서 세 번째 변의 길이를 뺀 몫입니다. 분모는 변경하지 않고 그대로 두겠습니다. 공식 형태로 보면 KA=2*√(MK*KB*P*(P-MB)) / (MK+KB)와 같습니다.

이등변삼각형의 이등분선은 일반적인 특성과 함께 몇 가지 고유한 특성도 갖습니다. 이것이 어떤 종류의 삼각형인지 기억해 봅시다. 이러한 삼각형은 밑면에 인접한 두 개의 동일한 변과 동일한 각도를 갖습니다. 이등변삼각형의 옆면에 있는 이등분선은 서로 같습니다. 또한, 밑변으로 내려간 이등분선은 높이이자 중앙값입니다.

오늘은 매우 쉬운 수업이 될 것입니다. 우리는 단 하나의 객체, 즉 각도 이등분선을 고려하고 미래에 우리에게 매우 유용할 가장 중요한 속성을 증명할 것입니다.

긴장을 풀지 마십시오. 동일한 통합 상태 시험 또는 통합 상태 시험에서 높은 점수를 받고 싶은 학생들이 첫 번째 수업에서 이등분선의 정의를 정확하게 공식화할 수도 없는 경우가 있습니다.

그리고 정말 흥미로운 일을 하는 대신에 우리는 이렇게 단순한 일에 시간을 낭비합니다. 그러니 읽고, 보고, 채택하세요. :)

우선 약간 이상한 질문이 있습니다. 각도란 무엇입니까? 맞습니다. 각도는 단순히 같은 지점에서 나오는 두 개의 광선입니다. 예를 들어:


각도의 예: 예각, 둔각, 직각

그림에서 볼 수 있듯이 각도는 예각, 둔각, 직선일 수 있습니다. 지금은 중요하지 않습니다. 종종 편의상 각 광선에 추가 점이 표시되며 우리 앞에 각도 $AOB$($\angle AOB$로 표시)이 있다고 말합니다.

Captain Obviousness는 $OA$ 및 $OB$ 광선 외에도 $O$ 지점에서 더 많은 광선을 그리는 것이 항상 가능하다는 것을 암시하는 것 같습니다. 그러나 그중에는 하나의 특별한 것이 있습니다. 그는 이등분선이라고 불립니다.

정의. 각도의 이등분선은 해당 각도의 꼭지점에서 나와 각도를 이등분하는 광선입니다.

위 각도의 경우 이등분선은 다음과 같습니다.


예각, 둔각, 직각에 대한 이등분선의 예

실제 도면에서는 특정 광선(우리의 경우 $OM$ 광선)이 원래 각도를 두 개의 동일한 각도로 분할한다는 것이 항상 명확하지 않기 때문에 기하학에서는 동일한 수의 호로 동일한 각도를 표시하는 것이 관례입니다( 우리 그림에서는 예각의 경우 호 1개, 둔각의 경우 호 2개, 직선의 경우 호 3개입니다.

좋아요, 정의를 정리했습니다. 이제 이등분선이 어떤 속성을 가지고 있는지 이해해야 합니다.

각도 이등분선의 주요 속성

실제로 이등분선에는 많은 속성이 있습니다. 그리고 우리는 다음 강의에서 그것들을 확실히 살펴볼 것입니다. 하지만 지금 당장 이해해야 할 한 가지 요령이 있습니다.

정리. 각도의 이등분선은 주어진 각도의 측면에서 등거리에 있는 점의 자취입니다.

수학에서 러시아어로 번역하면 이는 한 번에 두 가지 사실을 의미합니다.

  1. 특정 각도의 이등분선 위에 있는 모든 점은 이 각도의 변으로부터 같은 거리에 있습니다.
  2. 그 반대의 경우도 마찬가지입니다. 점이 주어진 각도의 측면에서 동일한 거리에 있으면 이 각도의 이등분선에 위치하는 것이 보장됩니다.

이러한 진술을 증명하기 전에 한 가지 점을 명확히합시다. 점에서 각도 측면까지의 거리를 정확히 무엇이라고 합니까? 여기서 점에서 선까지의 거리에 대한 오래된 결정이 우리에게 도움이 될 것입니다.

정의. 점에서 선까지의 거리는 주어진 점에서 이 선까지 그은 수직선의 길이입니다.

예를 들어 $l$ 선과 이 선 위에 있지 않은 점 $A$를 생각해 보세요. $H\in l$인 $AH$에 수직을 그립니다. 그러면 이 수직선의 길이는 $A$ 지점에서 $l$ 직선까지의 거리가 됩니다.

점에서 선까지의 거리를 그래픽으로 표현

각도는 단순히 두 개의 광선이고 각 광선은 직선 조각이므로 한 점에서 각도 측면까지의 거리를 쉽게 결정할 수 있습니다. 이것들은 단지 두 개의 수직선입니다:


점에서 각도의 변까지의 거리를 결정합니다.

그게 다야! 이제 우리는 거리가 무엇인지, 이등분선이 무엇인지 알았습니다. 그러므로 우리는 주요 속성을 증명할 수 있습니다.

약속한 대로, 우리는 증명을 두 부분으로 나눌 것입니다:

1. 이등분선의 점에서 각의 변까지의 거리는 같습니다.

꼭지점 $O$와 이등분선 $OM$이 있는 임의의 각도를 생각해 보세요.

바로 이 점 $M$이 각의 변으로부터 같은 거리에 있다는 것을 증명해 보겠습니다.

증거. $M$ 점에서 각도의 변까지 수직선을 그립니다. $M((H)_(1))$ 및 $M((H)_(2))$라고 부르겠습니다.

각도의 측면에 수직을 그립니다.

$\vartriangle OM((H)_(1))$ 및 $\vartriangle OM((H)_(2))$라는 두 개의 직각 삼각형을 얻었습니다. 공통 빗변 $OM$과 동일한 각도를 갖습니다.

  1. $\angle MO((H)_(1))=\angle MO((H)_(2))$ 조건에 따라 ($OM$은 이등분선이므로);
  2. $\angle M((H)_(1))O=\angle M((H)_(2))O=90()^\circ $ 구조;
  3. $\angle OM((H)_(1))=\angle OM((H)_(2))=90()^\circ -\angle MO((H)_(1))$, 이후 합계 직각삼각형의 예각은 항상 90도입니다.

결과적으로 삼각형은 측면과 인접한 두 각도가 동일합니다(삼각형의 동일 표시 참조). 따라서 특히 $M((H)_(2))=M((H)_(1))$, 즉 $O$ 지점에서 각 변까지의 거리는 실제로 동일합니다. Q.E.D.:)

2. 거리가 같으면 점은 이등분선에 위치합니다.

이제 상황은 역전되었습니다. 각도 $O$가 주어지고 이 각도의 측면에서 등거리에 있는 점 $M$이 있다고 가정합니다.

$OM$ 광선이 이등분선임을 증명해 보겠습니다. $\각 MO((H)_(1))=\각 MO((H)_(2))$.

증거. 먼저 이 광선 $OM$을 그려보겠습니다. 그렇지 않으면 증명할 것이 아무것도 없습니다.

코너 안쪽에 $OM$ 빔 전도

다시 우리는 $\vartriangle OM((H)_(1))$ 및 $\vartriangle OM((H)_(2))$라는 두 개의 직각 삼각형을 얻습니다. 분명히 그들은 다음과 같은 이유로 동일합니다:

  1. 빗변 $OM$ - 일반;
  2. 다리 $M((H)_(1))=M((H)_(2))$ 조건에 따라 (결국 $M$ 지점은 각도 측면에서 등거리에 있습니다);
  3. 나머지 다리도 동일하기 때문에 피타고라스 정리 $OH_(1)^(2)=OH_(2)^(2)=O((M)^(2))-MH_(1)^(2)$에 의해.

따라서 세 변에 $\vartriangle OM((H)_(1))$ 및 $\vartriangle OM((H)_(2))$ 삼각형이 있습니다. 특히, 그들의 각도는 동일합니다: $\angle MO((H)_(1))=\angle MO((H)_(2))$. 이는 $OM$이 이등분선임을 의미합니다.

증명을 마무리하기 위해 결과적으로 동일한 각도를 빨간색 호로 표시합니다.

이등분선은 $\angle ((H)_(1))O((H)_(2))$를 두 개의 동일한 각도로 나눕니다.

보시다시피 복잡한 것은 없습니다. 우리는 각의 이등분선이 이 각의 변과 같은 거리에 있는 점들의 궤적이라는 것을 증명했습니다. :)

이제 용어를 어느 정도 결정했으므로 다음 단계로 넘어갈 차례입니다. 다음 강의에서는 이등분선의 더 복잡한 속성을 살펴보고 이를 실제 문제 해결에 적용하는 방법을 배우겠습니다.

삼각형의 내각을 삼각형 이등분선이라고 합니다.
삼각형 각도의 이등분선은 꼭지점과 이등분선과 삼각형의 반대쪽 변의 교차점 사이의 선분으로도 이해됩니다.
정리 8. 삼각형의 세 이등분선은 한 점에서 교차합니다.
실제로, 먼저 두 이등분선(예: AK 1과 VK 2)의 교차점 P를 고려해 보겠습니다. 이 점은 각도 A의 이등분선에 있기 때문에 변 AB와 AC로부터 같은 거리에 있고, 각도 B의 이등분선에 속하므로 변 AB와 BC에서도 같은 거리에 있습니다. 변 AC와 BC는 세 번째 이등분선 CK 3에 속합니다. 즉, 점 P에서 세 이등분선이 모두 교차합니다.
삼각형의 내부 각도와 외부 각도의 이등분선의 속성
정리 9. 삼각형 내각의 이등분선은 반대쪽 변을 인접한 변에 비례하는 부분으로 나눕니다.
증거. 삼각형 ABC와 그 각 B의 이등분선을 생각해보자. 꼭지점 C를 통해 이등분선 BC에 평행한 직선 CM을 그려서 변 AB가 이어지는 점 M에서 교차할 때까지 그려보자. VC는 각 ABC의 이등분선이므로 ∠ ABC = ∠ KBC입니다. 또한, 평행선에 대한 해당 각도인 ∠ АВК=∠ ВСМ, 평행선에 대한 교차 각도인 ∠ КВС=∠ ВСМ입니다. 따라서 ∠ ВСМ=∠ ВМС이므로 삼각형 ВСМ는 이등변이므로 ВС=ВМ입니다. 각도의 변과 교차하는 평행선에 대한 정리에 따르면 AK:K C=AB:VM=AB:BC가 있으며, 이는 증명되어야 합니다.
정리 10 삼각형 ABC의 외각 B의 이등분선은 비슷한 특성을 갖습니다. 꼭지점 A와 C에서 이등분선과 변 AC의 연속 교점의 점 L까지의 선분 AL과 CL은 삼각형의 변에 비례합니다. : 알: C.L.=AB:기원전.
이 속성은 이전 속성과 동일한 방식으로 증명됩니다. 그림에서 보조선 SM은 이등분선 BL에 평행하게 그려집니다. 각 BMC와 BC가 같습니다. 이는 삼각형 BMC의 변 BM과 BC가 동일하다는 것을 의미합니다. 이로써 우리는 AL:CL=AB:BC라는 결론에 도달했습니다.

정리 d4. (이등분선의 첫 번째 공식): 만약 삼각형 ABC에서 선분 AL이 각 A의 이등분선이라면 AL은? = AB·AC - LB·LC.

증거: M을 선 AL과 삼각형 ABC에 외접하는 원의 교차점으로 설정합니다(그림 41). 각도 BAM은 조건에 따라 각도 MAC과 동일합니다. 각도 BMA와 BCA는 동일한 코드에 대응되는 내접 각도와 합동입니다. 이는 삼각형 BAM과 LAC가 두 각도에서 유사하다는 것을 의미합니다. 따라서 AL:AC = AB:AM이 됩니다. 따라서 AL · AM = AB · AC<=>AL (AL + LM) = AB AC<=>알? = AB · AC - AL · LM = AB · AC - BL · LC. 이것이 입증되어야 하는 것입니다. 참고: 원에서 교차하는 현의 세그먼트와 내접각에 대한 정리는 원과 원 주제를 참조하세요.

정리 d5. (이등분선에 대한 두 번째 공식): 변 AB=a, AC=b 및 각 A가 2인 삼각형 ABC에서? 그리고 이등분선 l, 등식은 다음과 같습니다:
l = (2ab / (a+b)) cos?.

증거: ABC를 주어진 삼각형, AL을 이등분선(그림 42), a=AB, b=AC, l=AL로 둡니다. 그러면 S ABC = S ALB + S ALC입니다. 그렇다면 압신2는? = 알신? +블신?<=>2absin?·cos? = (a + b) lsin?<=>l = 2·(ab / (a+b))· cos?. 정리가 입증되었습니다.



유사한 기사